I am a physcis PhD student at UC Berkeley in the final year of my studies. My interests are very broad, but I mostly focus on time-domain astronomy, statistics and machine learning. Here is a selection of my most exciting projects.

What does it take to scale MCMC to high dimensions?

High-dimensional Markov chain Monte Carlo (MCMC) is a common bottleneck in scientific applications, ranging from Bayesian inference to statistical physics and lattice field theories. I have led the development of Microcanonical Langevin Monte Carlo (MCLMC), which is the first ever out-of-the-box MCMC algorithm without Metropolis adjustment. Avoiding the adjustment gives it superior scaling with the dimensionality of the problem, while still maintaining error guarantees through a tuning scheme that I have developed.
It outperforms current state-of-the-art samplers like the No-U-Turn Sampler (NUTS). As an example, it has been applied to cosmological field level inference from galaxy surveys, with orders of magnitudes speed-ups observed: with 2 million parameters, MCLMC inference takes 4 hours while NUTS needs more than 3 days for the same accuracy and computational resources. The gains are growing further as the dimensionality increases. This is an important advance because it makes MCMC feasible in high-dimensional applications where approximate and often unreliable methods have been used, and opens up a new realm for applications. So far, I have started collaborating with groups working on Bayesian neural networks, molecular dynamics, lattice quantum chromodynamics, weather prediction, cosmology, and radiation image reconstruction, and I am looking forward to expanding the variety of problems further.

I am also working on a new methodology that takes advantage of GPU architectures, where parallel chains are run. My specific strategy is to first quickly converge close to the target distribution and then refine the solution to achieve fine convergence. This strategy was proposed in the mathematical literature, but it was not implemented in practice. Preliminary results with my implementation are excellent, suggesting that an accurate posterior can be obtained only in a few hundred gradient evaluations, suggesting that MCMC could even be applied to problems with extremely expensive likelihood evaluations, as long as they can be run on a GPU in parallel.

All of the code is publicly available as a part of the Blackjax package and comes with tutorials and a website. Julia implementation is also available. For reproducibility we have developed benchmarking code.

Occurence of Earth-like planets in the habitable zone

“How common are planets that can support life as we know it?” is one of the most fundamental questions in modern astronomy. Currently, we do not have a sufficient number of confirmed detections of terrestrial Earth-like planets in the habitable zone of Sun-like stars to enable measurements of their occurrence rate. Instead, the occurrence rate is measured for larger planets and extrapolated. My goal is to directly measure the occurrence rate by using probabilistic methods and to understand how the occurrence rate depends on the planet’s properties, such as eccentricity, as well as on its environment: stellar properties, presence of the other planets and stars in the system, etc. This will greatly improve our understanding of planet habitability, constrain the rocky planet formation theories, and guide the design and allocation time of the future exoplanet surveys.

As a first step, I have developed an exoplanet transit detection and vetting pipeline for Kepler data that is particularly tailored to the detection of small planets close to the detection limit. The pipeline maximises the true positive probability at a fixed false alarm rate by carefully treating various noise sources such as stellar variability, sudden pixel sensitivity drops, and outliers in a principled manner.

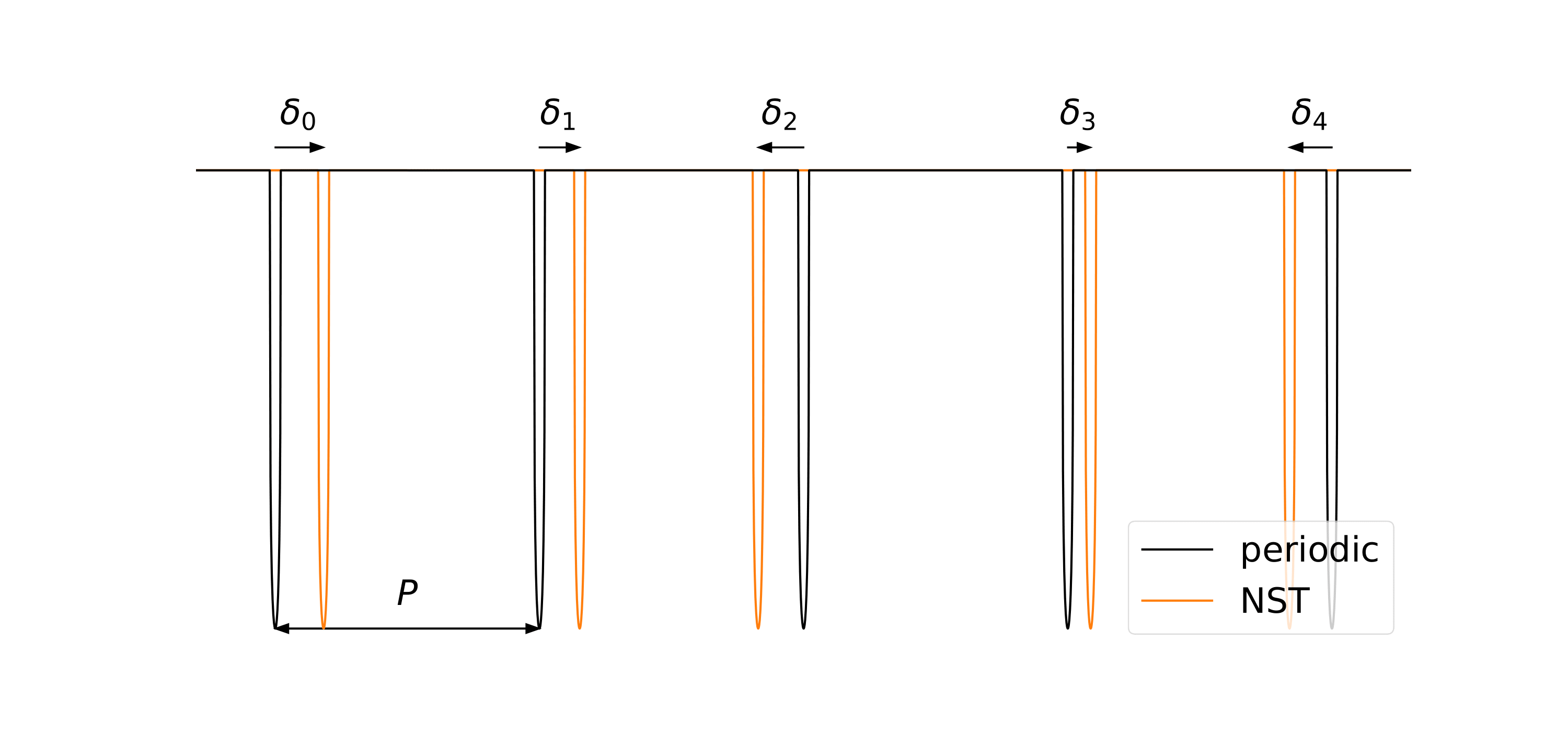The main strength of my approach, however, is the null signal template (NST) that I developed, and the robustness to the false alarms that it offers. NST is a signal template where planet transits have been perturbed to no longer be periodic. Reanalysis with NST serves as a null simulation, where true planets are not found (because they are periodic), but the false alarm distribution is the same as with the original periodic template. I have shown that this approach is more reliable than the currently established methods for estimating the false alarm probability. For example, this plot shows that NST is capable of reproducing the false alarm peak associated with rolling band systematics (at 370 days period), while state-of-the-art method called scarmbling fails: 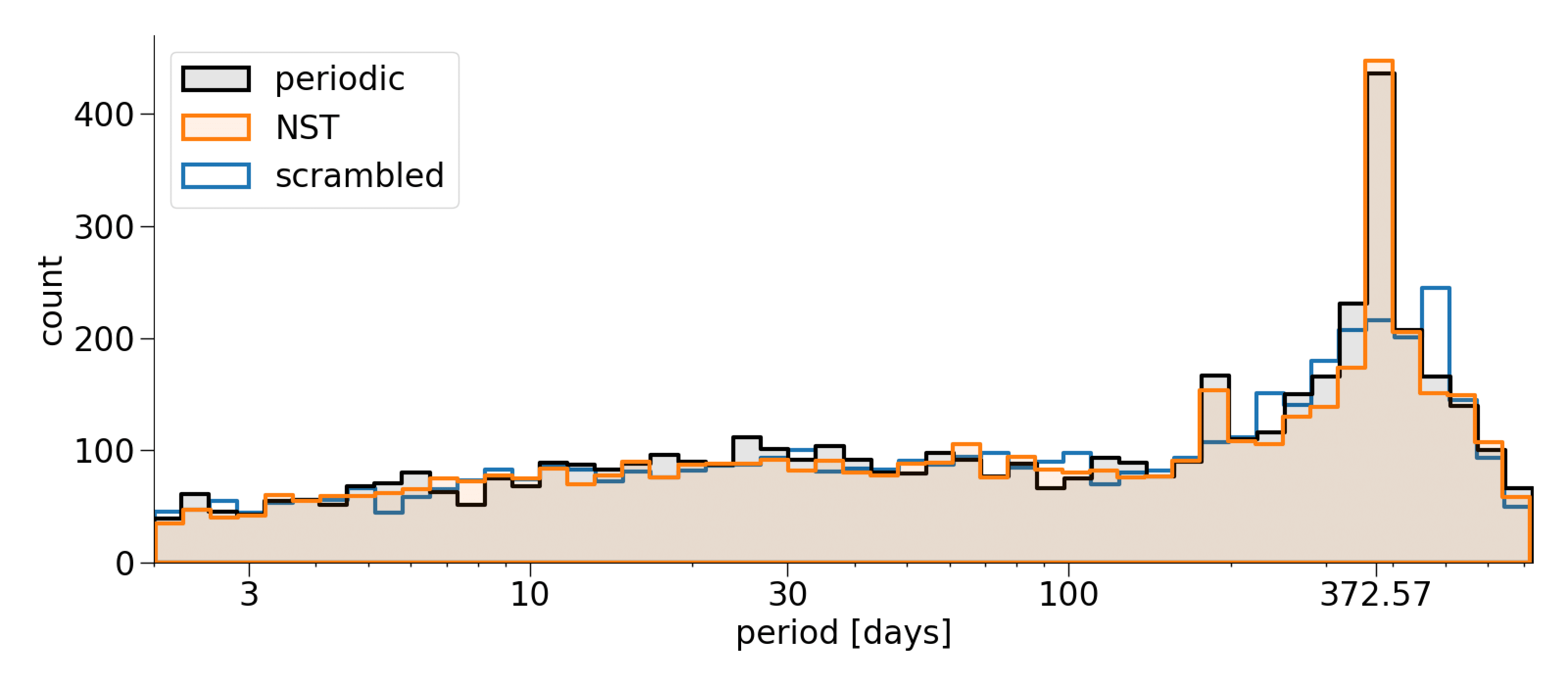This can have significant impact on the validation of exoplanet candidates and on the occurence rate.

With these developments, I have reevaluated the statistical significance of several Earth-like planets in the habitable zone and validated the most Earth-like planet in the Kepler data, Kepler 452-b. Using the NST approach, one can statistically take advantage of the planet candidates whose false alarm probability is not low enough for confirmation, and thus significantly increase the effective planet sample size, enabling the occurrence rate measurement down to Earth-like periods and radii.

Periodograms, supermassive black hole binaries and beyond

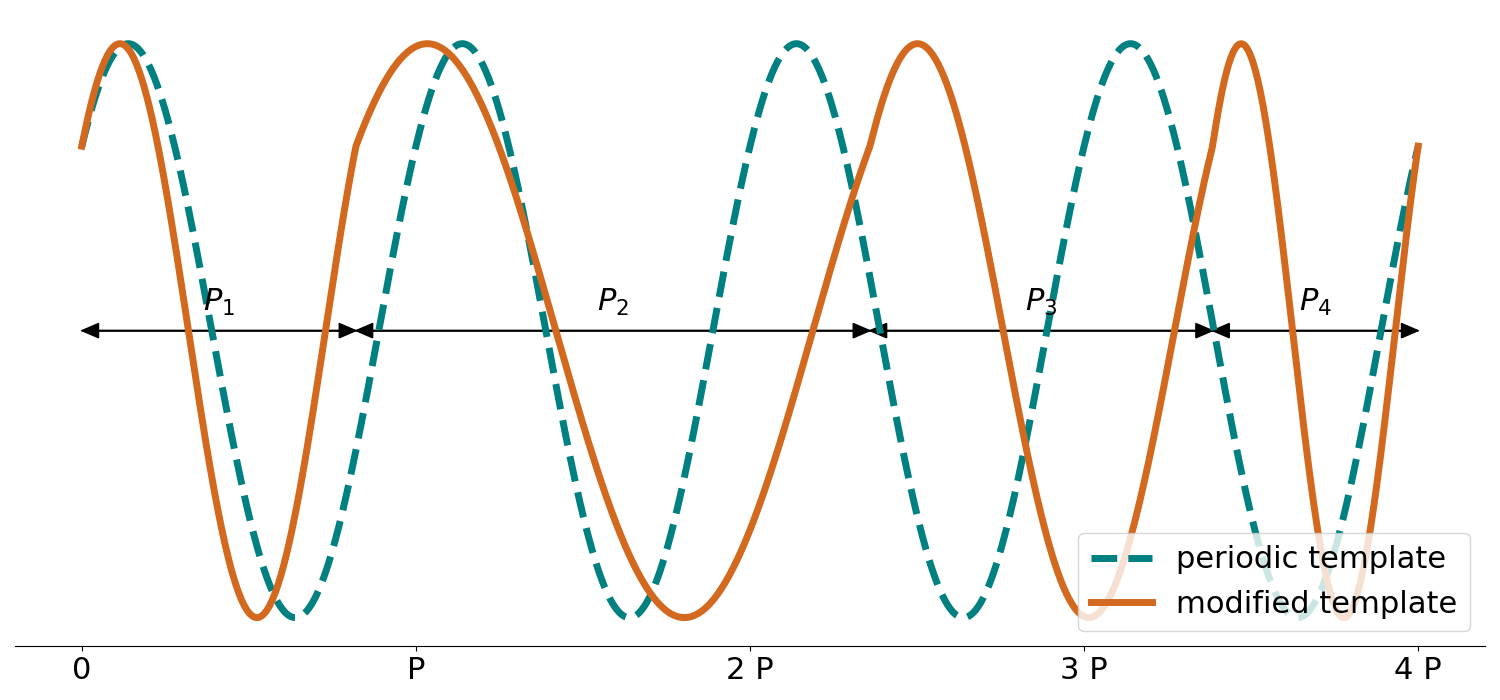The idea of null signal templates goes beyond the exoplanet search and can be applied to other time-series data. I have already applied it to periodicity significance testing in periodograms. The resulting python (JAX) package is publicly available. I applied this approach to the search for supermassive black hole binaries in the Palomar Transient Factory (PTF) data and demonstrated that the previously proposed candidates are likely to be false alarms. I am also applying it to the search for exomoons. Another interesting future direction I am pursuing is combining NST with a machine learning classifier, by training the classifier on the data with an injected signal and on an injected null signal, and then running both classifiers on the data to obtain a reliable false positive rate estimate.